Section 2.2 solutions
Exercise 2.17
In this exercise, we are tasked with creating a procedure last-pair and returns a list containing the last element of the list. It canbe done as follows:-
(define (last-pair items)
(if (null? (cdr items))
items
(last-pair (cdr items))))
; last-pair
(last-pair (list 23 72 149 34))
; (34)
(last-pair (list 23 72 149 (list 34 45)))
; ((34 45))Exercise 2.18
In this exercise, we are tasked with writing a procedure reverse which can be used to convert a list to another list with the same elements in reverse order. It can be done with the assistance of the append function given in the book.
(define (append list1 list2)
(if (null? list1)
list2
(cons (car list1)
(append (cdr list1)
list2))))
; append
(define (reverse items)
(if (null? items)
items
(append (reverse (cdr items))
(list (car items)))))
; reverse
(reverse (list 1 4 9 16 25))
; (25 16 9 4 1)Exercise 2.19
In this exercise, we are tasked with rewriting the change-counting program in Section 1.2.2 so that they can be used on arbitrary currency by allowing the denominations to be specified as a list. We are given the folowing function cc:-
(define (cc amount coin-values)
(cond ((= amount 0)
1)
((or (< amount 0)
(no-more? coin-values))
0)
(else
(+ (cc
amount
(except-first-denomination
coin-values))
(cc
(- amount
(first-denomination
coin-values))
coin-values)))))We are tasked with writing the procedures first-denomination, except-first-denomination and no-more? to complete the procedure. Let us do that and test the function.
(define first-denomination car)
(define except-first-denomination cdr)
(define no-more? null?)
(define us-coins
(list 50 25 10 5 1))
; us-coins
(define uk-coins
(list 100 50 20 10 5 2 1 0.5))
; uk-coins
(cc 100 us-coins)
; 292
(cc 100 uk-coins)
; 104561We can see that our solution gives the same right answer as before.
Further, we are asked if the order of the list coin-values affect the answer produced by cc or not. The answer is that it should not affect the answer. This is because our current algorithm checks all coin combinations irrespective of their denomination order. Let us test it.
(define us-coins-scr (list 10 25 1 50 5))
; us-coins-scr
(cc 100 us-coins-scr)
; 292As we can see, the same answer is obtained.
Exercise 2.20
In this exercise, we are tasked with using the dotted-tail notation to define a procedure same-parity which can be used to return a list of all arguments that has the same even-odd parity as the first argument.
(define (same-parity head . tail)
(let ((rem (remainder head 2)))
(define (filter-even-odd items)
(if (null? items)
items
(if (= (remainder (car items) 2) rem)
(cons (car items)
(filter-even-odd (cdr items)))
(filter-even-odd (cdr items)))))
(cons head (filter-even-odd tail))))
; same-parity
(same-parity 1 2 3 4 5 6 7)
; (1 3 5 7)
(same-parity 2 3 4 5 6 7)
; (2 4 6)Exercise 2.21
In this exercise, we are tasked with creating a procedure square-list by filling the missing expressions in the given procedures. The two procedures perform the operation directly and using map respectively. W
(define (square-list items)
(if (null? items)
nil
(cons (square (car items)) (square-list (cdr items)))))
; square-list
(square-list (list 1 2 3 4))
; (1 4 9 16)(define (square-list items)
(map square items))
; square-list
(square-list (list 1 2 3 4))
; (1 4 9 16)As can be seen, both definitions give the same correct answer. However, the second case would be a better definition because of its simplicity.
Exercise 2.22
In this exercise, we are tasked with determining why the square-list procedure written by Louis Reasoner does not exactly give the right answer.
Original code
The first iteration of the square-list procedure is as follows.
(define (square-list items)
(define (iter things answer)
(if (null? things)
answer
(iter (cdr things)
(cons (square (car things))
answer))))
(iter items nil))
; square-list
(square-list (list 1 2 3 4))
; (16 9 4 1)As can be seen, we get the expected result, but in reverse. To see how this happens, let us expand the evaluation.
(square-list (list 1 2 3 4))
(iter (list 1 2 3 4) nil)
(iter (list 2 3 4) (cons 1 nil))
(iter (list 3 4) (cons 4 (cons 1 nil)))
(iter (list 4) (cons 9 (cons 4 (cons 1 nil))))
(iter nil (cons 16 (cons 9 (cons 4 (cons 1 nil)))))
(cons 16 (cons 9 (cons 4 (cons 1 nil))))
(16 9 4 1)Thus, to fix this reversal, Louis tries to switch the arguement to cons.
Reversed code
Let us look at the reversed code and its execution.
(define (square-list items)
(define (iter things answer)
(if (null? things)
answer
(iter (cdr things)
(cons answer
(square
(car things))))))
(iter items nil))
; square-list
(square-list (list 1 2 3 4))
; ((((() . 1) . 4) . 9) . 16)Now the values appear in the right order but the lists appear wonky. Let us see why.
(square-list (list 1 2 3 4))
(iter (list 1 2 3 4) nil)
(iter (list 2 3 4) (cons nil 1))
(iter (list 3 4) (cons (cons nil 1) 4))
(iter (list 4) (cons (cons (cons nil 1) 4) 9))
(iter nil (cons (cons (cons (cons nil 1) 4) 9) 16))
(cons (cons (cons (cons nil 1) 4) 9) 16)
((((() . 1) . 4) . 9) . 16)Thus, we can see that this doesn’t work either because putting nil in the car position does not make it vanish.
Fixed code
Since we have the things in the right order, we can use our old friend append to make things appear as they should.
(define (square-list items)
(define (iter things answer)
(if (null? things)
answer
(iter (cdr things)
(append answer
(list (square (car things)))))))
(iter items nil))
; square-list
(square-list (list 1 2 3 4))
; (1 4 9 16)Thus, we have the right answer by eliminating the nil in the wrong places and flattening the list at each iteration.
Exercise 2.23
We are asked to implement a procedure called for-each in this exercise. This procedure takes a procedure and a list. The procedure does not evaluate to anything but simply perform an action. It can be done using the following code.
(define (for-each f items)
(if (null? items)
#t
(begin (f (car items))
(for-each f (cdr items)))))
; for-each
(for-each f (list 57 321 88))
; 57
; 321
; 88
; #tNote that begin is used to sequence the operations so that they can be executed together.
Exercise 2.24
In this exercise, we are asked to evaluate the expression (list 1 (list 2 (list 3 4))). Then, we are asked to provide the box-and-pointer structure and the tree interpretation of the result. Evaluating the expression, we get the following:-
(list 1 (list 2 (list 3 4)))
; (1 (2 (3 4)))The box-and-pointer structure is as follows:-

Likewise, the tree structure is as follows:-

Exercise 2.25
In this exercise, we are tasked with giving the combination of cars and cdrs required to pick 7 from the lists.
(1 3 (5 7) 9)
(define a (list 1 3 (list 5 7) 9))
; a
a
; (1 3 (5 7) 9)
(cdr a)
; (3 (5 7) 9)
(cdr (cdr a))
; ((5 7) 9)
(car (cdr (cdr a)))
; (5 7)
(cdr (car (cdr (cdr a))))
; (7)
(car (cdr (car (cdr (cdr a)))))
; 7((7))
(define b (list (list 7)))
; b
b
; ((7))
(car b)
; (7)
(car (car b))
; 7(1 (2 (3 (4 (5 (6 7))))))
(define c (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7)))))))
; c
c
; (1 (2 (3 (4 (5 (6 7))))))
(cdr c)
; ((2 (3 (4 (5 (6 7))))))
(car (cdr c))
; (2 (3 (4 (5 (6 7)))))
(cdr (car (cdr c)))
; ((3 (4 (5 (6 7)))))
(car (cdr (car (cdr c))))
; (3 (4 (5 (6 7))))
(cdr (car (cdr (car (cdr c)))))
; ((4 (5 (6 7))))
(car (cdr (car (cdr (car (cdr c))))))
; (4 (5 (6 7)))
(cdr (car (cdr (car (cdr (car (cdr c)))))))
; ((5 (6 7)))
(car (cdr (car (cdr (car (cdr (car (cdr c))))))))
; (5 (6 7))
(cdr (car (cdr (car (cdr (car (cdr (car (cdr c)))))))))
; ((6 7))
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr c))))))))))
; (6 7)
(cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr c)))))))))))
; (7)
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr c))))))))))))
; 7Note that we can write successive cars and cdrs upto four times using a short-hand notation. Eg. (cadadr x) for (car (cdr (car (cdr x)))) and so on.
Exercise 2.25
This exercise simply tasks us with finding out the result printed when evaluated by the interpreter.
(define x (list 1 2 3))
; x
(define y (list 1 2 3))
; y
x
; (1 2 3)
y
; (1 2 3)
(append x y)
; (1 2 3 1 2 3)
(cons x y)
; ((1 2 3) 1 2 3)
(list x y)
; ((1 2 3) (1 2 3))Exercise 2.27
In this exercise, we are tasked with modifying the reverse procedure from before to produce deep-reverse which reverses it elements and reverses all sublists as well.
Let us look at the original reverse procedure.
(define (reverse items)
(if (null? items)
items
(append (reverse (cdr items))
(list (car items)))))Similarly, deep-reverse can be defined as follows:-
(define (deep-reverse items)
(if (or (null? items)
(not (pair? items)))
items
(append (deep-reverse (cdr items))
(list (deep-reverse (car items))))))Let us test it.
(define x (list (list 1 2) (list 3 4)))
; x
x
; ((1 2) (3 4))
(reverse x)
; ((3 4) (1 2))
(deep-reverse x)
; ((4 3) (2 1))Works as predicted. Let us try with a more complex expression.
(define y (list (list 1 2) (list 3 4) (list (list 5 6) (list 7 8))))
; y
y
; ((1 2) (3 4) ((5 6) (7 8)))
(deep-reverse y)
; (((8 7) (6 5)) (4 3) (2 1))Exercise 2.28
In this exercise, we are tasked with writing a procedure fringe which takes a tree and returns the leaves arranged left-to-right. It can be accomplished using the following code:-
(define (fringe items)
(cond ((null? items) items)
((pair? items) (append (fringe (car items))
(fringe (cdr items))))
(else (list items))))Let us test the code using the same test cases as the previous exercise.
x
; ((1 2) (3 4))
(fringe x)
; (1 2 3 4)
(fringe (list x x))
; (1 2 3 4 1 2 3 4)
y
; ((1 2) (3 4) ((5 6) (7 8)))
(fringe y)
; (1 2 3 4 5 6 7 8)
(fringe (list y y))
; (1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8)Exercise 2.28
In this exercise, we are tasked with implementing binary mobile data structures.
A mobile is created by taking two branches and combining them.
(define (make-mobile left right)
(list left right))Further, a branch is created by compounding a length for the structure and the structure itself, which could be simple number or a mobile.
(define (make-branch length structure)
(list length structure))Branch selectors
Given a mobile, the branches can be selected using the following code:-
(define (left-branch mobile)
(car mobile))
(define (right-branch mobile)
(cadr mobile))With the branch selected, its length and structure can be obtained as follows:-
(define (branch-length branch)
(car branch))
(define (branch-structure branch)
(cadr branch))Weight calculation
The weight of a given mobile can be computed as follows:-
(define (total-weight mobile)
(+ (branch-weight (left-branch mobile))
(branch-weight (right-branch mobile))))
(define (branch-weight branch)
(let ((b (branch-structure branch)))
(if (pair? b)
(total-weight b)
b)))Balance verification
We can verify if a mobile is balanced using the following code:-
(define (balanced? mobile)
(and (= (branch-torque (left-branch mobile))
(branch-torque (right-branch mobile)))
(balanced-branch? (left-branch mobile))
(balanced-branch? (right-branch mobile))))
(define (branch-torque branch)
(* (branch-weight branch)
(branch-length branch)))
(define (balanced-branch? branch)
(let ((b (branch-structure branch)))
(if (pair? b)
(balanced? b)
#t)))Change of representation
When the representation of mobiles are changed to cons instead of list as follows,
(define (make-mobile left right)
(cons left right))
(define (make-branch length structure)
(cons length structure))Only the accessors need to be changed as follows,
(define (left-branch mobile)
(car mobile))
(define (right-branch mobile)
(cdr mobile))
(define (branch-length branch)
(car branch))
(define (branch-structure branch)
(cdr branch))Exercise 2.30
In this exercise, we are tasked with writing square-tree which is analogous to square-list which can be used to square all the elements in a list and maintain the overall structure of the list. Let us look at how to do this directly.
(define (square-tree tree)
(cond ((null? tree) tree)
((not (pair? tree)) (square tree))
(else (cons (square-tree (car tree))
(square-tree (cdr tree))))))
; square-tree
(square-tree
(list 1
(list 2 (list 3 4) 5)
(list 6 7)))
; (1 (4 (9 16) 25) (36 49))Now, this function could also be rewritten using the map function and recursion. Let us see how this is done:-
(define (square-tree tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(square-tree sub-tree)
(square sub-tree)))
tree))
; square-tree
(square-tree
(list 1
(list 2 (list 3 4) 5)
(list 6 7)))
; (1 (4 (9 16) 25) (36 49))Exercise 2.31
In this exercise, we are tasked with creating a procedure tree-map which serves the same purpose for as the map procedure does for lists. Let us define it using the code from the previous exercise as a template.
(define (tree-map proc tree)
(cond ((null? tree) tree)
((not (pair? tree)) (proc tree))
(else (cons (tree-map proc (car tree))
(tree-map proc (cdr tree))))))
; tree-map
(define (square-tree tree)
(tree-map square tree))
; square-tree
(square-tree
(list 1
(list 2 (list 3 4) 5)
(list 6 7)))
; (1 (4 (9 16) 25) (36 49))Exercise 2.32
The subsets function can be defined as follows by filling in the blanks.
(define (subsets s)
(if (null? s)
(list nil)
(let ((rest (subsets (cdr s))))
(append rest
(map (lambda (r)
(cons (car s) r))
rest)))))
; subsets
(subsets (list 1 2 3))
; (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))The definition of powerset here gives the exact algorithm used by us in our subsets procedure. To prove that this works, let us use the method of induction.
To prove that, let us take two axioms:-
(subset (cons x y))contains all the members of(subset y)- In
(subset (cons x y)), exactly half the members havex, since given any set, there is a 50/50 chance ofxbeing there.
Now, onto the proof:-
-
The subset of an empty list is a list of empty list. ie
(subset ())is(()). -
We assume for a list
y,(subset y)gives the correct set of subsets. We add one more element to the set to obtain(cons x y). By axiom 1,(subset y)gives all the subsets of(subset (cons x y))which does not contain the elementx. By axiom 2,(subset (cons x y))has exactly twice as many members as(subset y). Thus, we get the new set by duplicating the members of(subset y)withxthrown in.
By following this principle, we get the correct subsets function.
Exercise 2.33
In this exercise, we are tasked with rewriting map, append and length functions using accumulate.
map
The map function can be written as follows:-
(define (map p sequence)
(accumulate (lambda (x y) (cons (p x) y))
nil sequence))
; map
(map square (list 1 2 3 4 5))
; (1 4 9 16 25)append
The append function can be written as folows:-
(define (append seq1 seq2)
(accumulate cons seq2 seq1))
; append
(append (list 1 2 3) (list 4 5 6))
; (1 2 3 4 5 6)
(append () (list 1 2 3))
; (1 2 3)length
The length function can be written as follows:-
(define (length sequence)
(accumulate (lambda (x y) (+ y 1)) 0 sequence))
; length
(length (list 1 2 3 4))
; 4Exercise 2.34
In this exercise, we are tasked with evaluating a polynomial at the given value of x using Horner’s Rule which is a recursive procedure which evaluates the polynomial by evaluating it as .
The procedure is defined as follows:-
(define
(horner-eval x coefficient-sequence)
(accumulate
(lambda (this-coeff higher-terms)
(+ this-coeff (* higher-terms x)))
0
coefficient-sequence))
; horner-eval
(horner-eval 2 (list 1 3 0 5 0 1))
; 79Exercise 2.35
In this exercise, we are tasked with redefining the count-leaves procedure defined earlier as follows:-
(define (count-leaves x)
(cond ((null? x) 0)
((not (pair? x)) 1)
(else (+ (count-leaves (car x))
(count-leaves (cdr x))))))We are told to use the accumulate and map function in the redefinition. For that purpose, let us reuse the enumerate-tree given in the book:-
(define (enumerate-tree tree)
(cond ((null? tree) nil)
((not (pair? tree)) (list tree))
(else (append
(enumerate-tree (car tree))
(enumerate-tree (cdr tree))))))
; enumerate-tree
(define (count-leaves t)
(accumulate +
0
(map (lambda (x) 1)
(enumerate-tree t))))
; count-leaves
(define x (cons (list 1 2) (list 3 4)))
; x
(count-leaves (list x x))
; 8Exercise 2.36
In this exercise, we need to implement a procedure accumulate-n which takes a list of lists and returns an element-wise accumulation in the form of another list. We assume each sub-list in the argument and the resulting list has the same number of elements each.
(define (accumulate-n op init seqs)
(if (null? (car seqs))
nil
(cons (accumulate op init (map car seqs))
(accumulate-n op init (map cdr seqs)))))
; accumulate-n
(define s (list (list 1 2 3) (list 4 5 6) (list 7 8 9) (list 10 11 12)))
; s
s
; ((1 2 3) (4 5 6) (7 8 9) (10 11 12))
(accumulate-n + 0 s)
; (22 26 30)Exercise 2.37
In this exercise, we are tasked with implementing matrix operations. The initial dot product procedure is defined as follows:-
(define (dot-product v w)
(accumulate + 0 (map * v w)))
; dot-product
(dot-product (list 1 2 3 4) (list 5 6 7 8))
; 70Note that it is mentioned in the book that the map procedure used is the original once defined in Scheme which can take an arbitrary number of lists as arguments.
Matrix-vector multiplication
The matrix-vector multiplication can be defined as follows:-
(define (matrix-*-vector m v)
(map (lambda (row) (dot-product row v)) m))
; matrix-*-vector
(define m (list (list 1 2 3) (list 4 5 6) (list 7 8 9)))
; m
(define v (list 1 2 3))
; v
(matrix-*-vector m v)
; (14 32 50)Transpose function
The transpose function can be defined as follows:-
(define (transpose mat)
(accumulate-n cons nil mat))
; transpose
m
; ((1 2 3) (4 5 6) (7 8 9))
(transpose m)
; ((1 4 7) (2 5 8) (3 6 9))Matrix-matrix multiplication
The matrix-matrix multiplication can be defined as follows:-
(define (matrix-*-matrix m n)
(let ((cols (transpose n)))
(map (lambda (row) (matrix-*-vector cols row)) m)))
; matrix-*-matrix
(define n (list (list 9 8 7) (list 6 5 4) (list 3 2 1)))
; n
(matrix-*-matrix m n)
; ((30 24 18) (84 69 54) (138 114 90))All the computations were verified using WolframAlpha
Exercise 2.38
In this exercise we examine fold-left and fold-right procedures.
(define (fold-right op initial sequence)
(if (null? sequence)
initial
(op (car sequence)
(fold-right op initial (cdr sequence)))))
(define (fold-left op initial sequence)
(define (iter result rest)
(if (null? rest)
result
(iter (op result (car rest))
(cdr rest))))
(iter initial sequence))Other than the fact that fold-left is iterative whereas fold-right is recursive, we can test the difference in results by looking at the examples provided.
(fold-right / 1 (list 1 2 3))
; 3/2
(fold-left / 1 (list 1 2 3))
; 1/6
(fold-right list nil (list 1 2 3))
; (1 (2 (3 ())))
(fold-left list nil (list 1 2 3))
; (((() 1) 2) 3)As can be seen, we get totally different results for both cases. Let us look at the expansion of each expression,
(fold-right op initial (list a b c))
(op a (fold-right op initial (list b c)))
(op a (op b (fold-right op initial (list c))))
(op a (op b (op c (fold-right op initial ()))))
(op a (op b (op c initial)))(fold-left op initial (list a b c))
(iter initial (list a b c))
(iter (op intial a) (list b c))
(iter (op (op intial a) b) (list c))
(iter (op (op (op intial a) b ) c) ())
(op (op (op inital a) b ) c)Now, to get similar operations for both procedures, we need two properties:-
-
(op initial a)must be the same as(op a initial). This is evident when we try this operation on a list with one element. This property is called commutativity. -
(op (op a b) c)must be the same as(op a (op b c)). This is evident when we look at the final form of the expansions. This property is called associativity.
In the given example, the division function and list functions fulfilled neither properties. Let us try with a function that fulfils both cases:-
(fold-left * 1 (list 1 2 3))
; 6
(fold-right * 1 (list 1 2 3))
; 6Exercise 2.39
In this exercise, we are tasked with defining the reverse procedure using the fold-right and fold-left from before.
(define (reverse sequence)
(fold-right
(lambda (x y) (append y (list x))) nil sequence))
; reverse
(reverse (list 1 2 3))
; (3 2 1)
(define (reverse sequence)
(fold-left
(lambda (x y) (append (list y) x)) nil sequence))
; reverse
(reverse (list 1 2 3))
; (3 2 1)Exercise 2.40
In this exercise, we are told to define a procedure unique-pairs which takes an integer n and generates a sequence of pairs (i,j) where . Basically, we are told to encapsulate the part that generates the pairs in the given prime-sum-pairs procedure in the book.
(define (flatmap proc seq)
(accumulate append nil (map proc seq)))
; flatmap
(define (enumerate-interval i j)
(if (> i j)
nil
(cons i (enumerate-interval (+ i 1) j))))
; enumerate-interval
(define (unique-pairs n)
(flatmap (lambda (i)
(map (lambda (j)
(list i j))
(enumerate-interval 1 (- i 1))
))
(enumerate-interval 1 n)))
; unique-pairs
(unique-pairs 5)
; ((2 1) (3 1) (3 2) (4 1) (4 2) (4 3) (5 1) (5 2) (5 3) (5 4))We can thus simplify the prime-sum-pairs procedure as follows:-
(define (prime-sum-pairs n)
(map make-pair-sum
(filter prime-sum? (unique-pairs n))))Exercise 2.41
In this exercise, we need to write a procedure that generates triples consisting of threee integers i, j and k less than or equal to a given number n that sums to a given integer s.
Drawing from the lessons learnt in this section, we start with smaller components and build the solution up. First, we build a unique-triples function that builds triples while using unique-pairs function.
(define (unique-triples n)
(flatmap (lambda (i)
(map (lambda (j)
(cons i j))
(unique-pairs (- i 1))))
(enumerate-interval 1 n)))
; unique-triplets
(unique-triplets 5)
; ((3 2 1) (4 2 1) (4 3 1) (4 3 2) (5 2 1) (5 3 1) (5 3 2) (5 4 1) (5 4 2) (5 4 3))Next, we do our normal filtering using a function.
(define (makes-sum? triple s)
(= (accumulate + 0 triple) s))
; makes-sum?
(define (triples-sum n s)
(filter (lambda (triple) (makes-sum? triple s))
(unique-triples n)))
; triples-sum
(triples-sum 20 10)
; ((5 3 2) (5 4 1) (6 3 1) (7 2 1))Exercise 2.42
In this interesting exercise, we need to solve the “eight-queens puzzle”, where we try to place 8 queen pieces on a chess board in an arrangement that no queen is checking any other queen. A resursive solution is proposed which can generate all the solutions to the puzzle.
We are given the main code for solving this problem:-
(define (queens board-size)
(define (queen-cols k)
(if (= k 0)
(list empty-board)
(filter
(lambda (positions)
(safe? k positions))
(flatmap
(lambda (rest-of-queens)
(map (lambda (new-row)
(adjoin-position
new-row
k
rest-of-queens))
(enumerate-interval
1
board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))We are told to finish implementing the required data representations and sub-procedures for this problem.
Representation of positions
The first issue to be dealt with is creating a way to represent the position of a piece on the board. We can use our old knowledge to store the location as a (row, col) pair.
(define (make-position col row)
(cons col row))
(define (position-col position)
(car position))
(define (position-row position)
(cdr position))
(define (print-position position)
(define colchar
(integer->char
(+ (char->integer #\`) (position-col position))))
(display colchar)
(display (position-row position)))Further, we can represent the state of the board using a list of positions. Empty board can be represented as an empty list. Adding a new piece to the board is as simple as appending it.
(define empty-board ())
(define (adjoin-position new-row k rest-of-queens)
(append rest-of-queens (list (make-position k new-row))))
(define (print-board board)
(if (null? board)
(display "EMPTY")
(begin
(display "(")
(print-position (car board))
(for-each (lambda (pos)
(begin
(display " ")
(print-position pos)))
(cdr board))
(display ")")
(newline))))Safe positions
Every time we add a new queen piece to the board, we must check if the position is valid, ie, there is no queen checking the new piece. Checking only happens in two cases,
- Both pieces are in the same row
- Both pieces can be checked diagonally
If both pieces have the same column, we have no trouble.
We can create micro-procedures which check for this.
(define (same-row pos1 pos2)
(= (position-row pos1) (position-row pos2)))
(define (diag-check pos1 pos2)
(= (abs (- (position-row pos1) (position-row pos2)))
(abs (- (position-col pos1) (position-col pos2)))))
(define (same-piece pos1 pos2)
(= (position-col pos1) (position-col pos2)))
(define (unsafe-pos? pos1 pos2)
(if (same-piece pos1 pos2) #f
(or (same-row pos1 pos2)
(diag-check pos1 pos2))))With that defined, let us look at defining the safe? function.
(define (get-position k positions)
(car (filter (lambda (pos) (= (position-col pos) k))
positions)))
(define (safe? k positions)
(define pos-k (get-position k positions))
(define (safe-iter p)
(if (null? p)
#t
(if (unsafe-pos? (car p) pos-k)
#f
(safe-iter (cdr p)))))
(safe-iter positions))Putting it all together
Now that all the components are set-up, we can run the code to see the solutions.
(define (print-queens n)
(for-each print-board (queens n)))
; print-queens
(print-queens 1)
; (a1)
(print-queens 4)
; (a2 b4 c1 d3)
; (a3 b1 c4 d2)
(print-queens 5)
; (a1 b3 c5 d2 e4)
; (a1 b4 c2 d5 e3)
; (a2 b4 c1 d3 e5)
; (a2 b5 c3 d1 e4)
; (a3 b1 c4 d2 e5)
; (a3 b5 c2 d4 e1)
; (a4 b1 c3 d5 e2)
; (a4 b2 c5 d3 e1)
; (a5 b2 c4 d1 e3)
; (a5 b3 c1 d4 e2)As the board size increases, the number of solutions also increase. The exact length is given at OEIS A000170. As can be seen, the first ten solutions areas follows:-
(map (lambda (n)
(cons n (length (queens n))))
(enumerate-interval 1 10))
; ((1 . 1) (2 . 0) (3 . 0) (4 . 2) (5 . 10) (6 . 4) (7 . 40) (8 . 92) (9 . 352) (10 . 724))This matches the number in the webpage.
Exercise 2.43
In this exercise, we are told to quantify how slowly Louis Reasoner’s solution witll run compared to the original solution. The only difference is that the order of (queen-cols (- k 1)) and (enumerate-interval 1 board-size) has been reversed. This means that each time the flat-map is called, queen-cols would be called board-size times instead of only once before.
In the original case, for (queen-cols k), (queen-cols (- k 1)) is only called once and work proportional to board-size is done on it. Thus, the overall time complexity is .
However in Louis’ case, for (queen-cols k), (queen-cols (- k 1)) is called board-size times followed by work proportional to board-size done on it. Thus, the overall time complexity is .
Taking the original time taken as T, the new time taken would be .
For this set of exercises, MIT-Scheme was proven insufficient due to the inability to draw pictures. Instead, Racket was used along with the SICP Picture Language package.
This package can be invoked by typing (require (planet "sicp.ss" ("soegaard" "sicp.plt" 2 1))) in the Racket REPL.
Exercise 2.44
In this exercise, we are tasked with implementing up-split, a function analogous to the right-split given in the book. It makes the painter split and branch upwards as follows when (up-split painter n) is called.

The code can be written as follows:-
(define (up-split painter n)
(if (= n 0)
painter
(let ((smaller (up-split painter (- n 1))))
(below painter
(beside smaller smaller)))))(paint einstein)

(paint (up-split einstein 1))

(paint (up-split einstein 2))

Exercise 2.45
In this exercise, we are told to express both right-split and up-split as instances of a general splitting operation. It can be done as follows:-
(define (split op1 op2)
(define (splitter painter n)
(if (= n 0)
painter
(let ((smaller (splitter painter (- n 1))))
(op1 painter
(op2 smaller smaller)))))
splitter)
(define right-split (split beside below))
(define up-split (split below beside))(paint (up-split einstein 2))

(paint (right-split einstein 2))

Exercise 2.46
In this exercise, we are told to simply create a data structure holding a 2D vector. We follow our templates as usual.
(define (make-vect xcor ycor)
(cons xcor ycor))
(define (xcor-vect vect)
(car vect))
(define (ycor-vect vect)
(cdr vect))Now, to implement the other procedures:-
(define (add-vect v1 v2)
(make-vect (+ (xcor-vect v1) (xcor-vect v2))
(+ (ycor-vect v1) (ycor-vect v2))))
(define (sub-vect v1 v2)
(make-vect (- (xcor-vect v1) (xcor-vect v2))
(- (ycor-vect v1) (ycor-vect v2))))
(define (scale-vect s v)
(make-vect (* s (xcor-vect v))
(* s (ycor-vect v))))Let us test them to be sure.
(define u (make-vect 1 5))
(define v (make-vect 2 7))
u
; (1 . 5)
v
; (2 . 7)
(add-vect u v)
; (3 . 12)
(sub-vect u v)
; (-1 . -2)
(scale-vect 5 u)
; (5 . 25)Exercise 2.47
In this exercise, we are given two constructors for frames. With the two constructors, we are needed to provide appropriate selectors for each representation.
(define (make-frame origin edge1 edge2)
(list origin edge1 edge2))
(define (origin-frame frame)
(car frame))
(define (edge1-frame frame)
(cadr frame))
(define (edge2-frame frame)
(caddr frame))
(define f (make-frame (make-vect 1 1) (make-vect 2 1) (make-vect 1 2)))
f
; ((1 . 1) (2 . 1) (1 . 2))
(origin-frame f)
; (1 . 1)
(edge1-frame f)
; (2 . 1)
(edge2-frame f)
; (1 . 2)Let’s look at the next case.
(define (make-frame origin edge1 edge2)
(cons origin (cons edge1 edge2)))
(define (origin-frame frame)
(car frame))
(define (edge1-frame frame)
(cadr frame))
(define (edge2-frame frame)
(cddr frame))
(define f (make-frame (make-vect 1 1) (make-vect 2 1) (make-vect 1 2)))
f
; ((1 . 1) (2 . 1) 1 . 2)
(origin-frame f)
; (1 . 1)
(edge1-frame f)
; (2 . 1)
(edge2-frame f)
; (1 . 2)Exercise 2.48
In this exercise, we are tasked with creating a data structure for representing a segment.
(define (make-segment v1 v2)
(cons v1 v2))
(define (start-segment s)
(car s))
(define (end-segment s)
(cdr s))Exercise 2.49
In this exercise, we are told to use the segments->painter function to create shapes.
Outline
The outline of the designated frame can be drawn using four segments. (0,0) to (1,0), (1,0) to (1,1), (1,1) to (0,1) and (0,1) to (0,0).
(define outline
(segments->painter
(list
(make-segment
(make-vect 0 0)
(make-vect 0.99 0))
(make-segment
(make-vect 0.99 0)
(make-vect 0.99 0.99))
(make-segment
(make-vect 0.99 0.99)
(make-vect 0 0.99))
(make-segment
(make-vect 0 0.99)
(make-vect 0 0)))))(paint outline)

Note 0.99 was used instead of 1 so that lines show up in the image.
Cross
The cross can be drawn using just two segments. (0,0) to (1,1) and (1,0) to (0,1).
(define cross
(segments->painter
(list
(make-segment
(make-vect 0 0)
(make-vect 1 1))
(make-segment
(make-vect 1 0)
(make-vect 0 1)))))(paint cross)
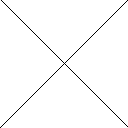
Diamond
The diamond can be constructed as follows:-
(define diamond
(segments->painter
(list
(make-segment
(make-vect 0 0.5)
(make-vect 0.5 0))
(make-segment
(make-vect 0.5 0)
(make-vect 1 0.5))
(make-segment
(make-vect 1 0.5)
(make-vect 0.5 1))
(make-segment
(make-vect 0.5 1)
(make-vect 0 0.5)))))(paint diamond)

Wave
Drawing the wave takes a bit longer. The coordinates are borrowed from Bill the lizard
(define wave
(segments->painter
(list
(make-segment
(make-vect 0.006 0.840)
(make-vect 0.155 0.591))
(make-segment
(make-vect 0.006 0.635)
(make-vect 0.155 0.392))
(make-segment
(make-vect 0.304 0.646)
(make-vect 0.155 0.591))
(make-segment
(make-vect 0.298 0.591)
(make-vect 0.155 0.392))
(make-segment
(make-vect 0.304 0.646)
(make-vect 0.403 0.646))
(make-segment
(make-vect 0.298 0.591)
(make-vect 0.354 0.492))
(make-segment
(make-vect 0.403 0.646)
(make-vect 0.348 0.845))
(make-segment
(make-vect 0.354 0.492)
(make-vect 0.249 0.000))
(make-segment
(make-vect 0.403 0.000)
(make-vect 0.502 0.293))
(make-segment
(make-vect 0.502 0.293)
(make-vect 0.602 0.000))
(make-segment
(make-vect 0.348 0.845)
(make-vect 0.403 0.999))
(make-segment
(make-vect 0.602 0.999)
(make-vect 0.652 0.845))
(make-segment
(make-vect 0.652 0.845)
(make-vect 0.602 0.646))
(make-segment
(make-vect 0.602 0.646)
(make-vect 0.751 0.646))
(make-segment
(make-vect 0.751 0.646)
(make-vect 0.999 0.343))
(make-segment
(make-vect 0.751 0.000)
(make-vect 0.597 0.442))
(make-segment
(make-vect 0.597 0.442)
(make-vect 0.999 0.144)))))(paint wave)
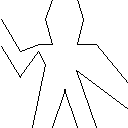
Exercise 2.50
In this exercise, we are tasked with defining the transformations to flip the painters horizontally, rotate them counterclockwise by 180 degrees and 270 degrees.
Let us start with the original coordinate system:-
The dotted outine refers to the area occupied by the frame with a square of length 1.
(paint einstein)

Horizontal flip
A horizontal flip can be done by using the following coordinate system for the frame:-
It can be done by defining the following transformation.
(define (flip-horizontal painter)
((transform-painter (make-vect 1.0 0.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0))
painter))(paint (flip-horizontal einstein))

Rotate counterclockwise by 180 degrees
A rotation by 180 degrees can be done using the following coordinate system:-
It can be done by defining the following transformation.
(define (rotate180 painter)
((transform-painter (make-vect 1.0 1.0)
(make-vect 0.0 1.0)
(make-vect 1.0 0.0))
painter))(paint (rotate180 einstein))
Rotate counterclockwise by 270 degrees
A rotation by 270 degrees can be done using the following coordinate system:-
It can be done by defining the following transformation.
(define (rotate270 painter)
((transform-painter (make-vect 0.0 1.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0))
painter))(paint (rotate270 einstein))

Exercise 2.51
In this exercise, we are tasked with writing an operation called below analogous to the beside operation given in the book. This procedure takes in two painters and places them one on top of another.
Direct method
The operation can be performed directly using the following code.
(define (below painter1 painter2)
(let ((split-point (make-vect 0.0 0.5)))
(let ((paint-bottom
((transform-painter (make-vect 0.0 0.0)
(make-vect 1.0 0.0)
split-point) painter1))
(paint-top
((transform-painter split-point
(make-vect 1.0 0.5)
(make-vect 0.0 1.0)) painter2)))
(lambda (frame)
(paint-bottom frame)
(paint-top frame)))))(paint (below einstein einstein))

Using beside and rotation
We can however, also utilise the given beside procedure coupled with rotation to achieve the same effect.
(define (below picture1 picture2)
(rotate90
(beside (rotate270 picture1)
(rotate270 picture2))))(paint (below einstein einstein))

Exercise 2.52
Through this exercise, we look at changing code at each abstraction level.
Adding smile
To add smile to the wave painter, I took the coordinates again from Bill the lizard.
(define wave-smile
(segments->painter
(list
(make-segment
(make-vect 0.006 0.840)
(make-vect 0.155 0.591))
(make-segment
(make-vect 0.006 0.635)
(make-vect 0.155 0.392))
(make-segment
(make-vect 0.304 0.646)
(make-vect 0.155 0.591))
(make-segment
(make-vect 0.298 0.591)
(make-vect 0.155 0.392))
(make-segment
(make-vect 0.304 0.646)
(make-vect 0.403 0.646))
(make-segment
(make-vect 0.298 0.591)
(make-vect 0.354 0.492))
(make-segment
(make-vect 0.403 0.646)
(make-vect 0.348 0.845))
(make-segment
(make-vect 0.354 0.492)
(make-vect 0.249 0.000))
(make-segment
(make-vect 0.403 0.000)
(make-vect 0.502 0.293))
(make-segment
(make-vect 0.502 0.293)
(make-vect 0.602 0.000))
(make-segment
(make-vect 0.348 0.845)
(make-vect 0.403 0.999))
(make-segment
(make-vect 0.602 0.999)
(make-vect 0.652 0.845))
(make-segment
(make-vect 0.652 0.845)
(make-vect 0.602 0.646))
(make-segment
(make-vect 0.602 0.646)
(make-vect 0.751 0.646))
(make-segment
(make-vect 0.751 0.646)
(make-vect 0.999 0.343))
(make-segment
(make-vect 0.751 0.000)
(make-vect 0.597 0.442))
(make-segment
(make-vect 0.597 0.442)
(make-vect 0.999 0.144))
(make-segment
(make-vect 0.395 0.916)
(make-vect 0.410 0.916))
(make-segment
(make-vect 0.376 0.746)
(make-vect 0.460 0.790)))))(paint wave-smile)
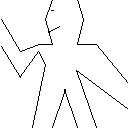
Change the corner-split pattern
We are tasked with modifying corner-split so that we only use up-split and right-split once. Let us try the original code:-
(paint (corner-split wave 2))

Now the modified code:-
(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1)))
(corner (corner-split painter (- n 1))))
(beside (below painter up)
(below right corner)))))(paint (corner-split wave 2))

Change of square-limit
We are told to change the square-limit function so that the larger segments are outside. We simply re-order things.
First let us look at the original diagram:-

(paint (square-limit wave 2))
(define (square-limit painter n)
(let ((combine4
(square-of-four flip-vert
rotate180
identity
flip-horiz)))
(combine4 (corner-split painter n))))(paint (square-limit wave 2))




